Operating Axioms, the Death March to the Quadratic Formula and an Unimpressed Student Teacher
Editor’s note: After a long hiatus because he teaches during the school year, Mr. Garelick returns once again in presenting the fourteenth chapter in a series called “Out on Good Behavior: Teaching Math While Looking Over Your Shoulder”. Garelick is a second-career math teacher in California. He has written articles on math education that have appeared in The Atlantic, Education Next, Education News and AMS Notices. He is also the author of three books on math education. Says Mr. Garelick: “At its completion, this series will be published in book form by John Catt Educational, Ltd. Also, to my devoted readers, I decided to name the first school I taught at as Cypress School rather than “my previous school” to reduce confusion and irritation with the author.” The previous chapters can be found here: Chapter 1 , Chapter 2 , Chapter 3 , Chapter 4 , Chapter 5, Chapter 6, Chapter 7, Chapter 8, Chapter 9, Chapter 10, Chapter 11, Chapter 12 and Chapter 13.

Ch 14 Operating Axioms, the Death March to the Quadratic Formula and an Unimpressed Student Teacher
In
math, assumptions held to be self-evident are accepted without proof and are
called axioms. In teaching, as in many situations in life, one also makes many
assumptions. I accept them without proof not because they are self-evident, but
because 1) they seem like they could be
true, and 2) I lack absolute proof. My axioms change from day to day depending
on circumstance and observation but eventually they coalesce into a consistent
set. Associated theorems then follow with the proviso that I could be dead
wrong.
During
my first year at Cypress I was forming many axioms particularly for my algebra
class. It was a small class—only 11 students—and included two sets of twin
girls. One set determined the tone of the class—they were somewhat dour and
projected a “don’t mess with me” vibe. The other twins were very bright, and
students clamored to be seated next to or near them whenever I changed the
seating.
The
class was unusually quiet and for the first few months I was always in doubt as
to where I stood with them. It wasn’t until about March when we hit the chapter
on quadratic equations that I felt I was hitting my stride with them.
At the start of the chapter
I announced that we would now be continuing on our death march to the quadratic
formula. “We’ve learned to solve some types of quadratic equations by
factoring, but now were going to look at more complicated cases when we can’t
factor,” I said. “By Friday of this week we will learn the quadratic formula.” I then wrote it on the board:
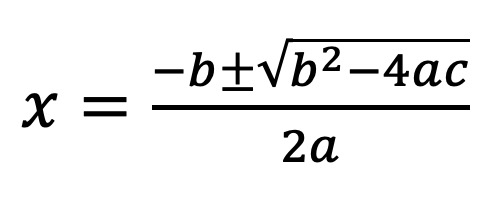
I tend to stay away from
things like posting “Today’s Objective” since most students ignore them as do
I. I find it far more effective to let them know what they’ll be doing in a
week’s time, or even a month’s. Plus the looks of horror and disbelief on their
faces tell me I have their attention. “By Friday this will not look as ominous
to you as it does now,” I said.
And sure enough, by the
time Friday came, and after working with solving quadratic equations by
completing the square, they were ready for the much easier way of solving
equations by the formula. After they felt comfortable with the formula I told
them that next week I would show them how the formula is derived.
“What does deriving the
formula mean?” one of the dour twins asked.
“It means solving the equation ax2 + bx + c = 0 using the steps of completing the square.”
Silence.
“And the derivation of the
quadratic formula will be an extra credit problem worth 10 points.”
“It must be hard,” the
other dour twin said.
“I don’t think it’s
hard,” I said. “If you can complete
the square, you can derive the formula.”
“I love completing the
square,” one of the bright twins said.
Earlier that week the third
grade teacher, Sandra, had asked me if the student teacher she was mentoring in
her class could observe one of my lessons.
“She’s interested in
teaching middle school math and wants to see a class.”
“She doesn’t want to teach
elementary school?” I asked.
“She’s exploring options.”
“Does she know what middle
school is like?”
“I think that’s why she wants
to observe a class,” Sandra said. Sandra had in fact taught algebra at Cypress
a few years before, team teaching with James, the union representative. An
opening for a third grade teacher came up and Sandra went for it, apparently
preferring it to middle school.
“Fine,” I said. “I’m
deriving the quadratic formula next Monday in my algebra class. Have her come by.”
The student teacher was in
her twenties and projected an aura of confidence that comes from a belief that
the (forgive me) crap ideas she had been fed in ed school were actually worth
following. (I’m assuming this as an axiom and feel fairly confident in doing
so.)
I started my lesson that
day by pointing to a poster I had made which bore a quote from Rene Descartes: “Each problem that I
solved became a rule which served afterwards to solve other problems.”
“Nowhere
is this more evident in Algebra 1 than in the derivation of the quadratic
formula,” I said, and proceeded to show the steps. The students knew how to complete the square,
having done it as part of last week’s death march. As I worked through the
derivation I asked them for the next steps. For the most part, they knew them,
though it often took some prodding on my part. I note that this is how I
normally teach but I was particularly aware of keeping up a dialogue lest I be
judged guilty of too much “teacher talk” as traditional teaching has come to be
characterized.
At the end of the class, the student teacher
left without a thank you—or anything. Her head was held obnoxiously high. I
assume but cannot prove that she thought that all I was doing was promoting
memorization and imitation of procedures, but not “deeper understanding”.
I never
heard from Sandra on what the student teacher might have thought. And in fact, I noticed that she was no longer as friendly to
me as she once had been. I assume (but cannot prove) that I was somehow
discredited in her eyes.
I did ask Sandra how her student teacher was
doing, hoping to get some feedback. “Oh,
she’s doing some innovative things in the class room,” she said. What these
innovative things were she didn’t say, nor did I ask. I assume with some degree
of confidence that it involved group work, collaboration, student-centered,
inquiry-based projects and not answering students’ questions.
As it stands, four out of my
eleven students got the derivation correct on the test. Two or three more got
partial credit for getting halfway through. I hold out belief that at least one
person was as fascinated as I was years ago in seeing how a method for solving
problems could be turned into a formula.
I have no proof of this of
course.
The post Operating Axioms, the Death March to the Quadratic Formula and an Unimpressed Student Teacher appeared first on Truth in American Education.






